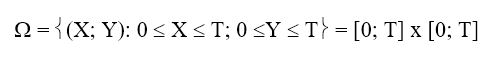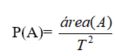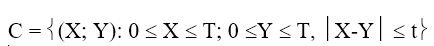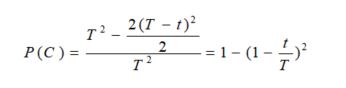INTRODUCCIÓN

Las probabilidades han tenido su origen en los juegos del azar y en la actualidad es de uso indispensable en el desarrollo de la humanidad. Las definiciones del concepto de probabilidades se puede estudiar considerando diferentes puntos de vistas como: frecuencial, clásico, geométrico, y axiomático. En todas esas definiciones existe una regularidad clarividente del concepto de probabilidad, que es necesaria para su mejor comprensión. En ese sentido, en este trabajo se abordan el método histórico lógico desde lo teórico y el análisis de documentos desde la empírea para discutir esas definiciones. Los resultados fundamentales están asociado a una caracterización de las definiciones expresadas, es decir, su origen, su contenido, ejemplo, sus dificultades y sus ventajas, esto propicia una mejor comprensión del tema y una apreciación del cómo responder a la problemática de impartir este andamiaje matemático. En síntesis, esta revisión pretende abordar aspectos importantes relacionados con la definición del concepto de probabilidades.

DESARROLLO

Curiosidades

¿Sabe usted la etimología de una pala­bra que es muy usada en el ámbito popular: azar?

La palabra, proviene del Árabe "Zahr", flor, la que se pintaba en una de las caras del dado.

 Alrededor de esta palabra es que giran las definiciones que a continuación se desarrollan en este trabajo:

Definición Frecuencial de Probabilidad.

Aspecto Histórico

En 1888 John Venn en “The logic  of  chance” defendió explícitamente el cálculo de probabilidad a partir de la frecuencia relativa y, en los tiempos modernos, Richard Von  Mises en  su libro “Probability, statistics an truth” 1919. También, Hans Reichenbach y Kolmogorov, son partidarios de este enfoque.

Definición

Designamos por A un suceso aleatorio que está en relación con un experimento aleatorio cualquiera. Se repite este experimento aleatorio n-veces, independiente una vez de otra, y se cuenta cuántas veces ocurre el suceso A en estos experimentos. Si A ocurre en total m-veces, entonces m se le llama frecuencia absoluta de A y m/n, frecuencia relativa de A en estos n experi­mentos. Gert Maibaum p.27

Dificultades    

Desde los puntos de vista filosófico, conceptual y práctico relacionada con la noción de número infinito de experi­mento.  No se puede calcular una probabilidad con precisión, porque el número de ensayos es siempre limitado (aunque la ley de los grandes números ofrece una cierta base).  Además, existen situaciones donde no es posible conducir ensayos repetidos bajo condiciones experimentales fijas.

Ventajas

En enseñanza elemental este enfoque es adecuado en la asignatura de Probabilidades. Por otro lado, el desarrollo de la computación facilita que los ensayos se realicen un número grande de veces y con una gran rapidez.

Si se desarrolla el experimento, una serie de veces independientes unas de las otras, y se calcula la frecuencia relativa a cada uno de ellos, se puede apreciar que estos números se diferencian poco unos de otros, véase el ejemplo clásico del Conde de Bufón en el lanzamiento de la moneda (tabla 1)

Definición Clásica de Probabilidad.

Aspecto Histórico:

Laplace en su obra "Teorie analitique des probabilités" (1812) es el primero en hablar del concepto de probabilidad.  Con frecuencia se considera a Pascal y Fermat como los iniciadores del Cálculo de Probabilidad. Pascal se interesa por este tema a propósito de cuestiones relativas a los juegos de azar que le propone el Caballero de Moró.

Definición:

Sea el punto de partida un experimento aleatorio con un número finito de resultados igualmente posibles, es decir, que no se diferencian con respecto al grado de indefinición de la ocurrencia.   Todo suceso aleatorio A en relación con el experimento aleatorio considerado, se puede caracterizar por la enumeración de aquellos resultados que son favorables para este suceso, es decir, que provocan su ocurrencia. Si designamos  con g(A) su número y con k(< infinito) el de todos los resultados,  entonces la  razón de g(A) y k proporciona una idea sobre el grado  de  la aparición  del  suceso  aleatorio A. En el marco de la llamada definición Clásica de Probabilidad, a este cociente se le llama probabilidad del suceso aleatorio A y se designa por p(A) (ecuación 1).

Gert Maibaum p.29

El espacio muestral tiene que ser finito y todos los sucesos que lo conforman tienen que ser equiprobables.  Es reducible solamente a problemas de análisis combinatorio, es circular y restrictivo, no responde a la pregunta qué es probabilidad, sino, que proporciona un método práctico de cálculo de probabilidades.

Ventajas

Se puede resolver una gran cantidad de ejercicios sencillos por el método que proporciona.

Definición Geométrica de Probabilidad

El Conde de Buffon es quien da el primer ejemplo de Probabilidad Geométrica con el famoso problema de la aguja de Buffon el cual fue publicado en la obra de G.L. Leclerc con el título de “Essai d'arithmetiquemorale” en 1733.

Definición

El experimento aleatorio debe entenderse como el modelo de la tirada aleatoria de un punto sobre el dominio básico E cualquiera del espacio Euclidiano n-dimensional, donde la palabra aleatoria debe entenderse de modo que:
1- El punto lanzado pueda caer sobre todo punto arbitrario de E.

2- Los sucesos aleatorios A y B a los cuales corresponden domi¬nios parciales de igual medida (intervalos de igual longitud, conjunto de punto del plano de igual área, cuerpo en el espacio tridimensional de igual volumen), posean también la misma proba¬bilidad, se calcula la probabilidad de un suceso A, que está en relación con un experimento semejante, según la ecuación 2.

Dificultades             

Sólo se puede calcular probabilidad, por esta fórmula, cuando sea entendida como "lanzar un punto a".

Ventajas        

Siempre que se conozca el espacio en el cual se está trabajando el cálculo se hace muy sencillo. Fue una primera extensión de la definición de Laplace para ser usada en el cálculo de probabilidades de espacios muéstrales infinitos. Ejemplo de esta definición lo constituye el “Problema del Encuentro”. Dos personas acuerdan encontrarse en un lugar determinado en el intervalo de tiempo [0; T]. Cada una de las personas elige el momento de llegada independientemente una de otra. Sea X e Y el tiempo de llegada de cada persona, respectivamente. Entonces el espacio maestral es el conjunto 1

Que representa un cuadrado de lado T.

Se considera al inicio, en calidad de sucesos aleatorios, todos los polígonos que están contenidos en omega. Se conoce que la clase K de tales polígonos es un Álgebra de sucesos. Asignémosles a cada polígono A de K la probabilidad, ecuación 3.

“Las personas se encontraron suponiendo que la primera que llega espera a la otra un tiempo t (t<T) y después se va”

Luego conjunto 2  y ecuación 4.

Ecuación 4

Primeramente, es conveniente hacer el siguiente cambio en la notación. Se considera ahora que “u” es el tiempo de llegada de una persona y “v” es el tiempo de llegada de la otra persona al lugar convenido, luego conjunto 3 y ecuación 5.

Ecuación 5

Esta es la función a través de la cual se puede calcular la probabilidad de este ejemplo en sentido general.

Definición Axiomática de Probabilidad

Aspecto Histórico                   

Kolmogorov (1933), fue quien dio por primera vez esta definición, la que fue traducida al inglés con el título de "Foundations of the theory of probability". Surge ante las restricciones del concepto clásico de probabilidad que imponía la equiprobabilidad de los sucesos y la finitud del espacio muestral correspondiente a dichos sucesos.

Definición:               

Sea Α un Álgebra de sucesos. Decimos que sobre Α está definida una probabilidad P (o una medida de probabilidad), si P es una función con las propiedades señaladas en los siguientes axiomas.

Axioma 1.

Dificultades               

No resulta muy fácil buscar el modelo para calcular la probabilidad de un experimento aleatorio dado.

Ventajas          

Los sucesos se representan por conjuntos y la probabilidad es una medida normada definidas sobre estos conjuntos. Este fundamento proporcionó no sólo un fundamento lógico para el cálculo de probabilidad, sino, que también la conectó con la corriente principal de la Matemática moderna. De todo lo desarrollado anteriormente, debemos definir, que desde el punto de vista formal-axiomático, la probabilidad es un objeto que satisface unos determinados axiomas, obteniendo los resultados teóricos mediante deducciones lógicas. Según Ma Moliner, Probabilidad se define como cualidad de probable o circunstancia de ser probable una cosa. El siguiente ejemplo muestra una "deficiencia" de la definción axiomática, aunque es bueno destacar que en todas las definiciones se encuentran “deficiencias”.

CONCLUSIONES

Se ha realizado una caracterización, desde el puno de vista histórico y pedagógico, del recorrido por el cual ha transitado el concepto de probabilidad y donde se evidencian las principales ventajas y desventajas de la del mismo.

La metodología del cómo se ha tratado este concepto constituye un elemento novedoso en esta socialización debido a que los textos utilizados para estos fines tratan una u otra definición, pero es difícil que hagan un estudio de todas las que se han definido en el decurso histórico.